1. 题目描述
在一个 n x n 的整数矩阵 grid 中,每一个方格的值 grid[i][j] 表示位置 (i, j) 的平台高度。
当开始下雨时,在时间为 t 时,水池中的水位为 t 。你可以从一个平台游向四周相邻的任意一个平台,但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离,也就是默认在方格内部游动是不耗时的。当然,在你游泳的时候你必须待在坐标方格里面。
你从坐标方格的左上平台 (0,0) 出发。返回 你到达坐标方格的右下平台 (n-1, n-1) 所需的最少时间 。
示例 1:
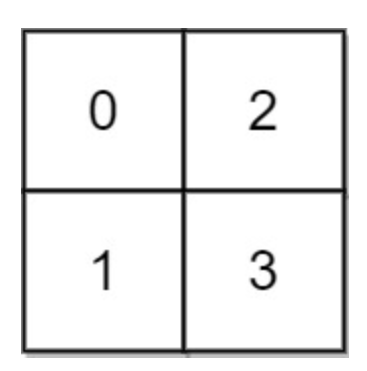
输入: grid = [[0,2],[1,3]] 输出: 3 解释: 时间为0时,你位于坐标方格的位置为 (0, 0)。 此时你不能游向任意方向,因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。 等时间到达 3 时,你才可以游向平台 (1, 1). 因为此时的水位是 3,坐标方格中的平台没有比水位 3 更高的,所以你可以游向坐标方格中的任意位置
示例 2:
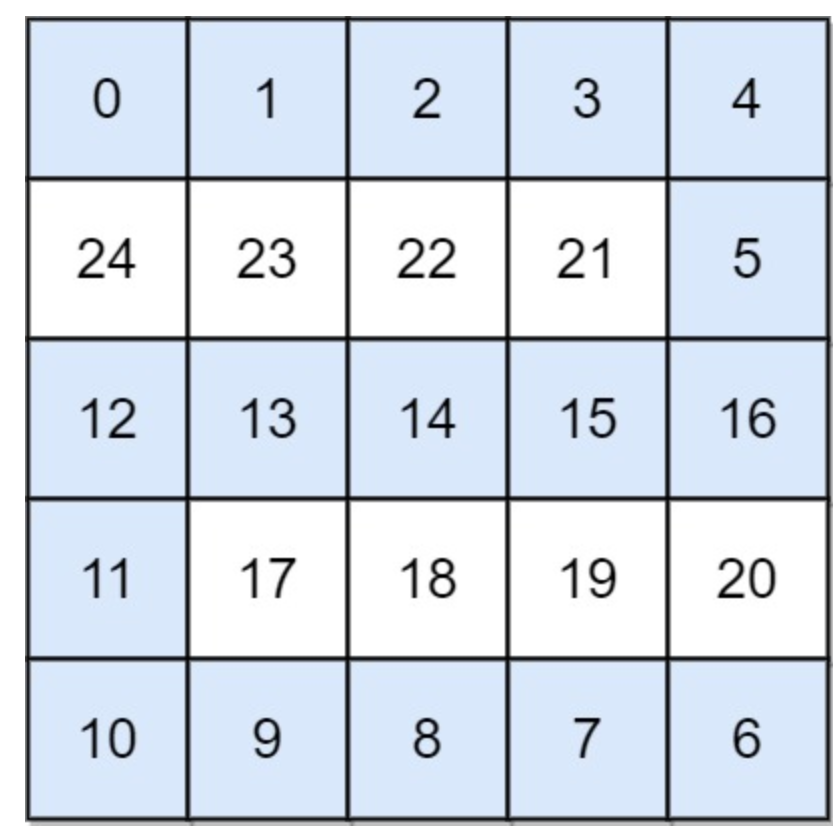
输入: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]] 输出: 16 解释: 最终的路线用加粗进行了标记。 我们必须等到时间为 16,此时才能保证平台 (0, 0) 和 (4, 4) 是连通的
提示:
2. 分析
核心思路:可达性搜索+记忆化+优先队列。
题意转化为:从(0,0)平台出发,到达(m-1,n-1)。作可达性搜索,每次取贡献值最小的备选节点作更新和记忆化搜索。
3. 代码
3.1. 搜索+自定义排序
type Point struct {
x, y int
}
var directions = [][]int{
{0, 1}, {-1, 0}, {0, -1}, {1, 0},
}
func swimInWater(grid [][]int) int {
m, n := len(grid), len(grid[0])
ans := grid[0][0]
aim := Point{x: m - 1, y: n - 1}
pq := []Point{{0, 0}}
// 记忆化
mem := map[Point]bool{}
mem[Point{0, 0}] = true
for len(pq) > 0 {
p := pq[0]
pq = pq[1:]
// 是否需要更新ans
ans = max(ans, grid[p.x][p.y])
// 到达目标值
if p == aim {
break
}
for _, direct := range directions {
np := Point{
x: p.x + direct[0],
y: p.y + direct[1],
}
// 边界和记忆化检查
if np.x < 0 || np.x >= m || np.y < 0 || np.y >= n || mem[np] {
continue
}
mem[np] = true
pq = append(pq, np)
}
sort.Slice(pq, func(i, j int) bool {
pi := pq[i]
pj := pq[j]
return grid[pi.x][pi.y] < grid[pj.x][pj.y]
})
}
return ans
}3.2. 记忆化搜索+优先队列(小根堆)
type Point struct {
x, y int
}
var directions = [][]int{
{0, 1}, {-1, 0}, {0, -1}, {1, 0},
}
type PriorityQueue struct {
vals []Point
grid [][]int
}
func (pq PriorityQueue) Len() int {
return len(pq.vals)
}
func (pq PriorityQueue) Swap(i, j int) {
pq.vals[i], pq.vals[j] = pq.vals[j], pq.vals[i]
}
// 小根堆
func (pq PriorityQueue) Less(i, j int) bool {
pi := pq.vals[i]
pj := pq.vals[j]
return pq.grid[pi.x][pi.y] < pq.grid[pj.x][pj.y]
}
func (pq *PriorityQueue) Pop() interface{} {
val := pq.vals[pq.Len()-1]
pq.vals = pq.vals[:pq.Len()-1]
return val
}
func (pq *PriorityQueue) Push(v interface{}) {
pq.vals = append(pq.vals, v.(Point))
}
func swimInWater(grid [][]int) int {
m, n := len(grid), len(grid[0])
ans := grid[0][0]
pq := &PriorityQueue{
vals: make([]Point, 0),
grid: grid,
}
aim := Point{x: m - 1, y: n - 1}
heap.Push(pq, Point{0, 0})
// 记忆化
mem := map[Point]bool{}
mem[Point{0, 0}] = true
for pq.Len() > 0 {
p := heap.Pop(pq).(Point)
// 是否需要更新ans
ans = max(ans, grid[p.x][p.y])
// 到达目标值
if p == aim {
break
}
for _, direct := range directions {
np := Point{
x: p.x + direct[0],
y: p.y + direct[1],
}
// 边界和记忆化检查
if np.x < 0 || np.x >= m || np.y < 0 || np.y >= n || mem[np] {
continue
}
mem[np] = true
heap.Push(pq, np)
}
}
return ans
}
评论