N皇后问题

Leetcode链接

1.题目描述

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数 n ，返回所有不同的 n 皇后问题的解决方案。每一种解法包含一个不同的 n 皇后问题的棋子放置方案，该方案’Q’’.’分别代表了皇后和空位。*
示例1：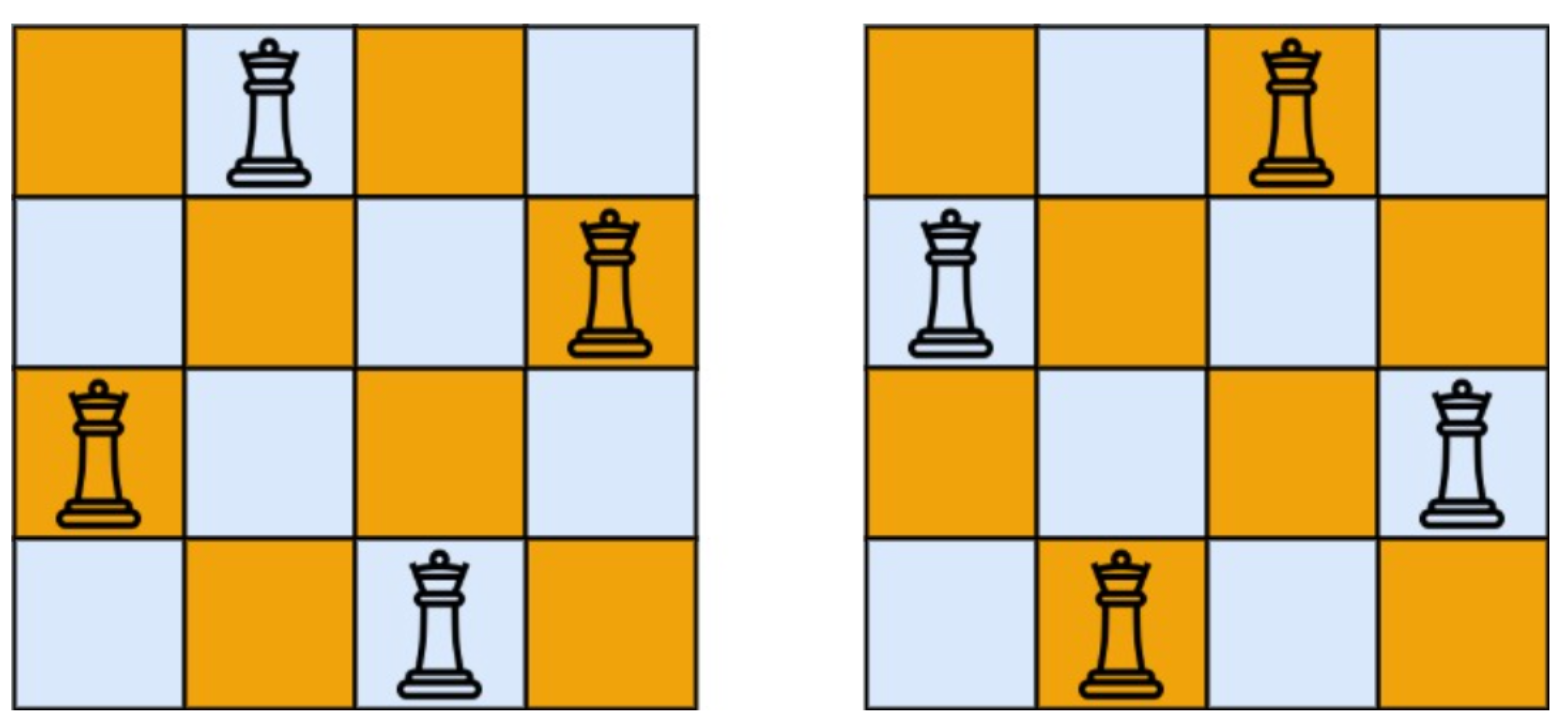

输入：n=4

输出：[[“.Q..”,”…Q”,”Q…”,”..Q.”],[“..Q.”,”Q…”,”…Q”,”.Q..”]]

解释：如上图所示，4皇后问题存在两个不同的解法。

提示：1<=n<=9

2.分析

此题使用 回溯 解决。

核心思路：遍历每一行 ，为每一行 选择合适的列 放置。

难点： 记忆化回溯。

N皇后问题，要求放置的皇后不能同行，同列，同对角线。

我们设计为每一行选择一列，设计算法保证了不会同行。

列的记忆化简单：mem0[col] 即可。

难点：对角线记忆化。

主对角线(左上角->右下角)，所有元素满足row-col 相等，记录mem1[row-col] 。

负对角线(左下角->右上角)，所有元素满足row+col 相等，记录mem2[row+col] 。

3.代码

特别说明：

由于本题值域较小，个人习惯使用数组作记忆化。使用hash表，由于表底层设计，hash冲突，扩表等，性能会劣于直接计算索引方式，当然本题量级小，损失小，可以忽略，取决于个人习惯。

// 一共n行n列
func solveNQueens(n int) [][]string {
    // 使用hash表更清晰，但计算慢
    mem0 := make([]bool, n)
    // 对角线的值域为2n, 主对角线把负值域变为正 key改为 row-col+n
    mem1 := make([]bool, 2*n)
    mem2 := make([]bool, 2*n)
    // ans 二维数组，记录x个答案，其中每个答案记录每行选择的列的位置
    ans := [][]int{}
    // 习惯定义匿名函数，这样不用将mem当多个参数传入
    var backtrack func(row int, chosen []int)
    backtrack = func(row int, chosen []int) {
        // 到达边界，得到一组答案，更新
        if len(chosen) == n {
            ans = append(ans, append([]int(nil), chosen...))
            return
        }
        // 到达边界, 没有选到答案
        if row == n {
            return
        }
        // 为当前行选择列
        for col := 0; col < n; col++ {
            //  记忆化，列、对角线被选择过，跳过
            if mem0[col] || mem1[row-col+n] || mem2[row+col] {
            continue
            }
            // 选择当前列作为第row行的选择
            mem0[col] = true
            mem1[row-col+n] = true
            mem2[row+col] = true
            // 继续递归回溯
            backtrack(row+1, append(chosen, col))
            // 当前递归结束，恢复
            mem0[col] = false
            mem1[row-col+n] = false
            mem2[row+col] = false
        }
    }
    // 从第0行开始递归选择
    backtrack(0, []int{})
    // 此时得到ans，包含每个结果，每个结果包含每行选择的列
    // 按照题意翻译为字符串数组即可
    strAns := make([][]string, len(ans))
    for i, cols := range ans {
        strAns[i] = parse(cols, n)
    }
    return strAns
}

// 将我们所求解的结果列翻译为答案要求的字符串

func parse(cols []int, n int) []string {
    ret := make([]string, n)
    for i := range ret {
        // 第i行选择第col列
        col := cols[i]
        // 翻译
        byts := make([]byte, n)
        for j := range byts {
            if j == col {
                byts[j] = 'Q'
            } else {
                byts[j] = '.'
            }
        }
        ret[i] = string(byts)
    }
    return ret
}

~

4.N皇后II

在N皇后问题的基础上，解决N皇后II则更简单了。

func totalNQueens(n int) int {
    // 使用hash表更清晰，但计算慢
    mem0 := make([]bool, n)
    // 对角线的值域为2n, 主对角线把负值域变为正 key改为 row-col+n
    mem1 := make([]bool, 2*n)
    mem2 := make([]bool, 2*n)
    // 只关心方案数
    ans := 0
    // 只关心方案数，chosen得到选择就加一
    var backtrack func(row int, chosen int)
    backtrack = func(row int, chosen int) {
        // 到达边界，得到一组答案，更新
        if chosen == n {
           ans++
           return
        }
        // 到达边界, 没有选到答案
        if row == n {
            return
        }
        // 为当前行选择列
        for col := 0; col < n; col++ {
            //  记忆化，列、对角线被选择过，跳过
            if mem0[col] || mem1[row-col+n] || mem2[row+col] {
                continue
            }
            // 选择当前列作为第row行的选择
            mem0[col] = true
            mem1[row-col+n] = true
            mem2[row+col] = true
            // 继续递归回溯
            backtrack(row+1, chosen+1)
            // 当前递归结束，恢复
            mem0[col] = false
            mem1[row-col+n] = false
            mem2[row+col] = false
        }
    }
    // 从第0行开始递归选择
    backtrack(0, 0)
    return ans
}

​