1. 题目描述

给你一个下标从 0 开始、大小为 m x n 的整数矩阵 matrix ，新建一个下标从 0 开始、名为 answer 的矩阵。使 answer 与 matrix 相等，接着将其中每个值为 -1 的元素替换为所在列的 最大 元素。

返回矩阵 answer 。

示例 1：

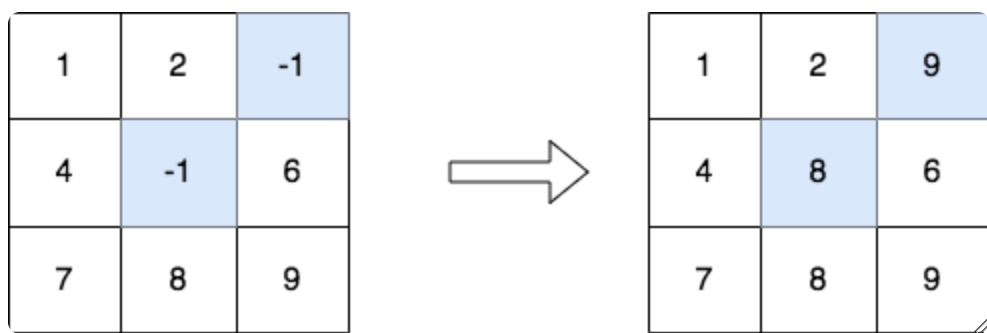
输入：matrix = [[1,2,-1],[4,-1,6],[7,8,9]]

输出：[[1,2,9],[4,8,6],[7,8,9]]

解释：上图显示了发生替换的元素（蓝色区域）。

• 将单元格 [1][1] 中的值替换为列 1 中的最大值 8 。

• 将单元格 [0][2] 中的值替换为列 2 中的最大值 9 。

示例 2：

输入：matrix = [[3,-1],[5,2]]

输出：[[3,2],[5,2]]

解释：上图显示了发生替换的元素（蓝色区域）。

提示：

• m == matrix.length

• n == matrix[i].length

• 2 <= m, n <= 50

• -1 <= matrix[i][j] <= 100

• 测试用例中生成的输入满足每列至少包含一个非负整数。

2. 分析

核心思路：记忆化加协程异步更新！

3. 代码

// 每个-1替换为所在列的最大值
func modifiedMatrix(matrix [][]int) [][]int {
	wg := sync.WaitGroup{}
	for j := 0; j < len(matrix[0]); j++ {
		m, vals := -1, make([]int, 0)
		for i := 0; i < len(matrix); i++ {
			if matrix[i][j] == -1 {
				vals = append(vals, i)
				continue
			}
			m = max(m, matrix[i][j])
		}
		wg.Add(1)
		go func(j int) {
			defer wg.Done()
			for _, idx := range vals {
				matrix[idx][j] = m
			}
		}(j)
	}
	wg.Wait()
	return matrix
}