链接直达

1. 题目描述

给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。

每次「迁移」操作将会引发下述活动：

• 位于 grid[i][j]（j < n - 1）的元素将会移动到 grid[i][j + 1]。

• 位于 grid[i][n - 1] 的元素将会移动到 grid[i + 1][0]。

• 位于 grid[m - 1][n - 1] 的元素将会移动到 grid[0][0]。

请你返回 k 次迁移操作后最终得到的 二维网格。

示例 1：

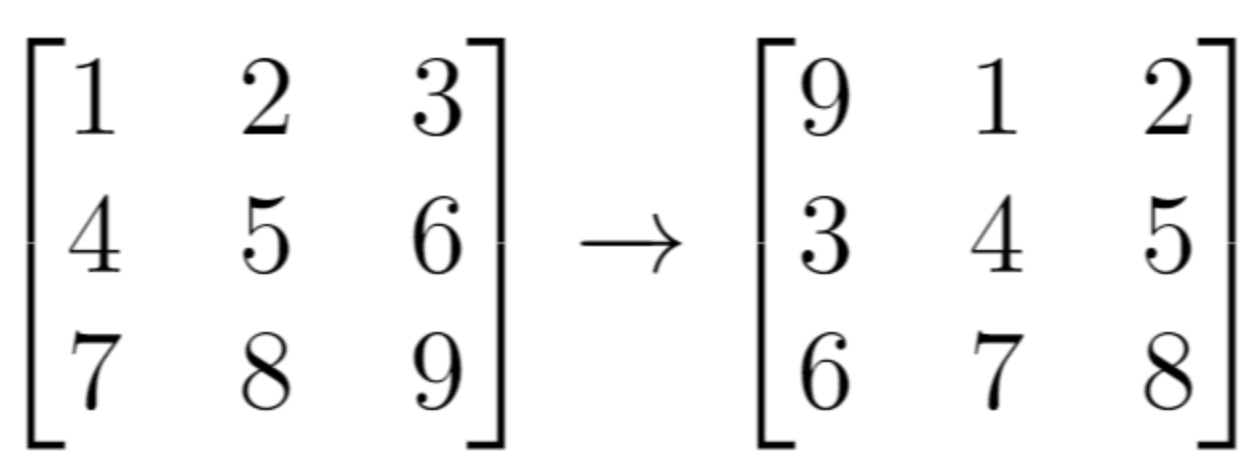
输入：grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1 输出：[[9,1,2],[3,4,5],[6,7,8]]

示例 2：

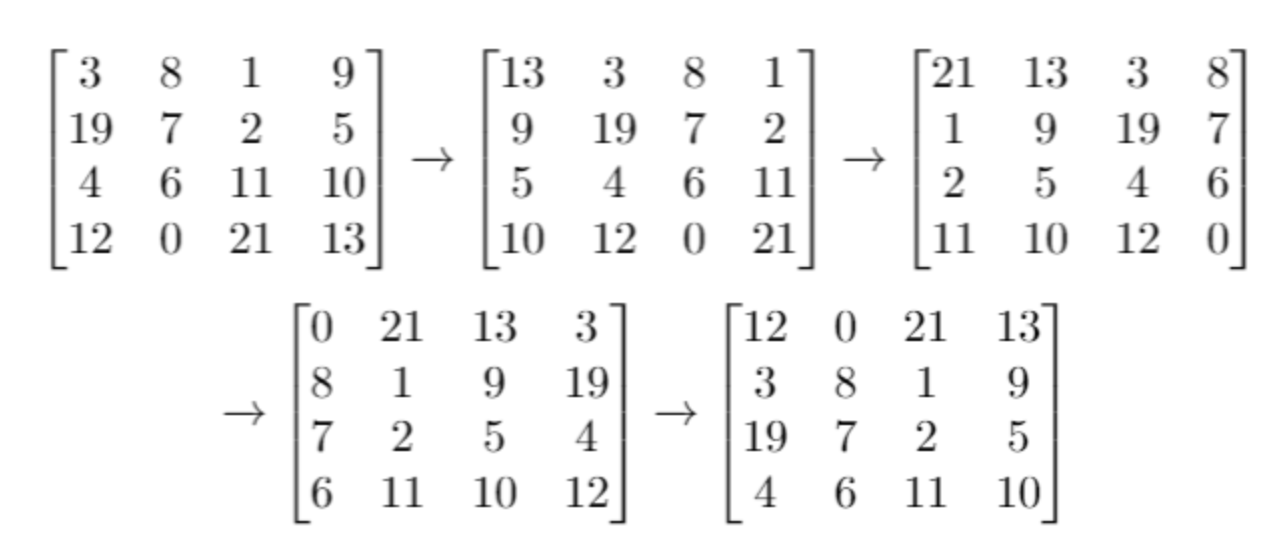
输入：grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4 输出：[[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

示例 3：

输入：grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9 输出：[[1,2,3],[4,5,6],[7,8,9]]

提示：

• m == grid.length

• n == grid[i].length

• 1 <= m <= 50

• 1 <= n <= 50

• -1000 <= gridi <= 1000

• 0 <= k <= 100

2. 分析

核心思路：原地置换，联通分量搜索。

原地置换算法

1. 通过当前节点计算下一个位置，更新下一个位置，继续...

2. 因为所有元素都移动k步，所以是定长的跨步，一定会返回开始节点。

3. 每遍历一圈，则是一个连通分量。

4. 如果一圈结束，总元素total没有被访问完，则继续 starti, startj+1 访问。

3. 代码

func shiftGrid(grid [][]int, k int) [][]int {
	m, n := len(grid), len(grid[0])
	// 总共应该m*n个位置
	total := m * n
	for i := range grid {
		for j := range grid[i] {
			startI := i
			startJ := j
			cnt := 1
			temp := grid[i][j]
			ii, jj := i, j
			for {
				row := (ii + (jj+k)/n) % m
				col := (jj + k) % n
				// 交换并被分temp
				temp, grid[row][col] = grid[row][col], temp
				if row == startI && col == startJ {
					total -= cnt
					// 连通分量清空
					if total == 0 {
						return grid
					}
					break
				}
				cnt++
				ii, jj = row, col
			}
		}
	}
	return nil
}